Let
be a cyclic quadrilateral. Let
,
,
be the feet of the perpendiculars from
to the lines
,
,
, respectively. Show that
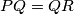
if and only if the bisectors of
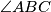
and
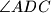
are concurrent with
.
%V0
Let $ABCD$ be a cyclic quadrilateral. Let $P$, $Q$, $R$ be the feet of the perpendiculars from $D$ to the lines $BC$, $CA$, $AB$, respectively. Show that $PQ=QR$ if and only if the bisectors of $\angle ABC$ and $\angle ADC$ are concurrent with $AC$.
Školjka