Slični zadaci
Regard a plane with a Cartesian coordinate system; for each point with integer coordinates, draw a circular disk centered at this point and having the radius 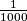 .
.
a) Prove the existence of an equilateral triangle whose vertices lie in the interior of different disks;
b) Show that every equilateral triangle whose vertices lie in the interior of different disks has a sidelength 96.
Radu Gologan, Romania
Remark
[The " 96" in (b) can be strengthened to " 124". By the way, part (a) of this problem is the place where I used the well-known "Dedekind" theorem.]
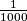 .
. a) Prove the existence of an equilateral triangle whose vertices lie in the interior of different disks;
b) Show that every equilateral triangle whose vertices lie in the interior of different disks has a sidelength 96.
Radu Gologan, Romania
Remark
[The " 96" in (b) can be strengthened to " 124". By the way, part (a) of this problem is the place where I used the well-known "Dedekind" theorem.]
Let  be an isosceles triangle with
be an isosceles triangle with 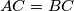 , whose incentre is
, whose incentre is  . Let
. Let  be a point on the circumcircle of the triangle
be a point on the circumcircle of the triangle 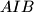 lying inside the triangle
lying inside the triangle  . The lines through
. The lines through  parallel to
parallel to  and
and 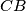 meet
meet  at
at  and
and  , respectively. The line through
, respectively. The line through  parallel to
parallel to  meets
meets  and
and 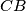 at
at  and
and  , respectively. Prove that the lines
, respectively. Prove that the lines 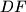 and
and 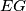 intersect on the circumcircle of the triangle
intersect on the circumcircle of the triangle  .
.
comment
(According to my team leader, last year some of the countries wanted a geometry question that was even easier than this...that explains IMO 2003/4...)
[Note by Darij: This was also Problem 6 of the German pre-TST 2004, written in December 03.]
Edited by Orl.
 be an isosceles triangle with
be an isosceles triangle with 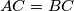 , whose incentre is
, whose incentre is  . Let
. Let  be a point on the circumcircle of the triangle
be a point on the circumcircle of the triangle 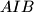 lying inside the triangle
lying inside the triangle  . The lines through
. The lines through  parallel to
parallel to  and
and 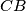 meet
meet  at
at  and
and  , respectively. The line through
, respectively. The line through  parallel to
parallel to  meets
meets  and
and 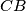 at
at  and
and  , respectively. Prove that the lines
, respectively. Prove that the lines 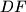 and
and 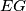 intersect on the circumcircle of the triangle
intersect on the circumcircle of the triangle  .
. comment
(According to my team leader, last year some of the countries wanted a geometry question that was even easier than this...that explains IMO 2003/4...)
[Note by Darij: This was also Problem 6 of the German pre-TST 2004, written in December 03.]
Edited by Orl.
In the coordinate plane consider the set  of all points with integer coordinates. For a positive integer
of all points with integer coordinates. For a positive integer  , two distinct points
, two distinct points  ,
, 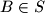 will be called
will be called  -friends if there is a point
-friends if there is a point 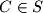 such that the area of the triangle
such that the area of the triangle  is equal to
is equal to  . A set
. A set 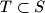 will be called
will be called  -clique if every two points in
-clique if every two points in  are
are  -friends. Find the least positive integer
-friends. Find the least positive integer  for which there exits a
for which there exits a  -clique with more than 200 elements.
-clique with more than 200 elements.
Proposed by Jorge Tipe, Peru
 of all points with integer coordinates. For a positive integer
of all points with integer coordinates. For a positive integer  , two distinct points
, two distinct points  ,
, 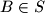 will be called
will be called  -friends if there is a point
-friends if there is a point 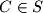 such that the area of the triangle
such that the area of the triangle  is equal to
is equal to  . A set
. A set 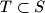 will be called
will be called  -clique if every two points in
-clique if every two points in  are
are  -friends. Find the least positive integer
-friends. Find the least positive integer  for which there exits a
for which there exits a  -clique with more than 200 elements.
-clique with more than 200 elements. Proposed by Jorge Tipe, Peru
 Školjka
Školjka  ,
, 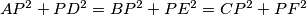 .
. 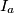 ,
, 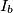 ,
, 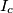 be the excenters of triangle
be the excenters of triangle 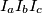 .
. 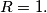 Let
Let  be the inradius of
be the inradius of  be the inradius of the orthic triangle
be the inradius of the orthic triangle 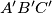 of triangle
of triangle  Prove that
Prove that 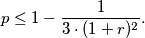
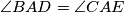 . If
. If  and
and  are, respectively, the points of tangency of the incircles of the triangles
are, respectively, the points of tangency of the incircles of the triangles 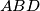 and
and 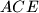 with the line
with the line 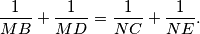
 and
and 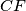 are altitudes. Two circles passing through the point
are altitudes. Two circles passing through the point  anf
anf  so that
so that  lies between
lies between  and
and 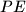 and
and 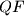 intersect on the circumcircle of triangle
intersect on the circumcircle of triangle 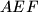 .
.