Let

be a prime number. Prove that there exists a prime number
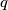
such that for every integer

, the number
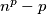
is not divisible by
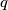
.
%V0
Let $p$ be a prime number. Prove that there exists a prime number $q$ such that for every integer $n$, the number $n^p-p$ is not divisible by $q$.