Slični zadaci
A pile of  pebbles is placed in a vertical column. This configuration is modified according to the following rules. A pebble can be moved if it is at the top of a column which contains at least two more pebbles than the column immediately to its right. (If there are no pebbles to the right, think of this as a column with 0 pebbles.) At each stage, choose a pebble from among those that can be moved (if there are any) and place it at the top of the column to its right. If no pebbles can be moved, the configuration is called a final configuration. For each
pebbles is placed in a vertical column. This configuration is modified according to the following rules. A pebble can be moved if it is at the top of a column which contains at least two more pebbles than the column immediately to its right. (If there are no pebbles to the right, think of this as a column with 0 pebbles.) At each stage, choose a pebble from among those that can be moved (if there are any) and place it at the top of the column to its right. If no pebbles can be moved, the configuration is called a final configuration. For each  , show that, no matter what choices are made at each stage, the final configuration obtained is unique. Describe that configuration in terms of
, show that, no matter what choices are made at each stage, the final configuration obtained is unique. Describe that configuration in terms of  .
.
IMO ShortList 2001, combinatorics problem 7, alternative
 pebbles is placed in a vertical column. This configuration is modified according to the following rules. A pebble can be moved if it is at the top of a column which contains at least two more pebbles than the column immediately to its right. (If there are no pebbles to the right, think of this as a column with 0 pebbles.) At each stage, choose a pebble from among those that can be moved (if there are any) and place it at the top of the column to its right. If no pebbles can be moved, the configuration is called a final configuration. For each
pebbles is placed in a vertical column. This configuration is modified according to the following rules. A pebble can be moved if it is at the top of a column which contains at least two more pebbles than the column immediately to its right. (If there are no pebbles to the right, think of this as a column with 0 pebbles.) At each stage, choose a pebble from among those that can be moved (if there are any) and place it at the top of the column to its right. If no pebbles can be moved, the configuration is called a final configuration. For each  , show that, no matter what choices are made at each stage, the final configuration obtained is unique. Describe that configuration in terms of
, show that, no matter what choices are made at each stage, the final configuration obtained is unique. Describe that configuration in terms of  .
. IMO ShortList 2001, combinatorics problem 7, alternative
For any integer 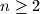 , we compute the integer
, we compute the integer 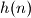 by applying the following procedure to its decimal representation. Let
by applying the following procedure to its decimal representation. Let  be the rightmost digit of
be the rightmost digit of  .
.
If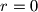 , then the decimal representation of
, then the decimal representation of 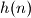 results from the decimal representation of
results from the decimal representation of  by removing this rightmost digit
by removing this rightmost digit  .If
.If 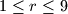 we split the decimal representation of
we split the decimal representation of  into a maximal right part
into a maximal right part  that solely consists of digits not less than
that solely consists of digits not less than  and into a left part
and into a left part  that either is empty or ends with a digit strictly smaller than
that either is empty or ends with a digit strictly smaller than  . Then the decimal representation of
. Then the decimal representation of 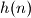 consists of the decimal representation of
consists of the decimal representation of  , followed by two copies of the decimal representation of
, followed by two copies of the decimal representation of 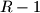 . For instance, for the number
. For instance, for the number 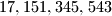 , we will have
, we will have 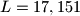 ,
, 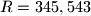 and
and 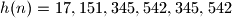 .Prove that, starting with an arbitrary integer
.Prove that, starting with an arbitrary integer 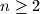 , iterated application of
, iterated application of  produces the integer
produces the integer  after finitely many steps.
after finitely many steps.
Proposed by Gerhard Woeginger, Austria
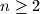 , we compute the integer
, we compute the integer 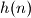 by applying the following procedure to its decimal representation. Let
by applying the following procedure to its decimal representation. Let  be the rightmost digit of
be the rightmost digit of  .
.If
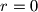 , then the decimal representation of
, then the decimal representation of 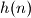 results from the decimal representation of
results from the decimal representation of  by removing this rightmost digit
by removing this rightmost digit  .If
.If 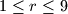 we split the decimal representation of
we split the decimal representation of  into a maximal right part
into a maximal right part  that solely consists of digits not less than
that solely consists of digits not less than  and into a left part
and into a left part  that either is empty or ends with a digit strictly smaller than
that either is empty or ends with a digit strictly smaller than  . Then the decimal representation of
. Then the decimal representation of 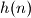 consists of the decimal representation of
consists of the decimal representation of  , followed by two copies of the decimal representation of
, followed by two copies of the decimal representation of 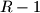 . For instance, for the number
. For instance, for the number 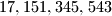 , we will have
, we will have 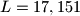 ,
, 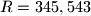 and
and 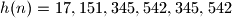 .Prove that, starting with an arbitrary integer
.Prove that, starting with an arbitrary integer 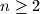 , iterated application of
, iterated application of  produces the integer
produces the integer  after finitely many steps.
after finitely many steps.Proposed by Gerhard Woeginger, Austria
 Školjka
Školjka  , let
, let 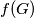 be the number of triangles and
be the number of triangles and 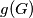 the number of tetrahedra formed by edges of
the number of tetrahedra formed by edges of  such that
such that 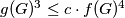
 and
and  play a game, given an integer
play a game, given an integer  ,
, 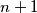 or
or  , but his number cannot be bigger than
, but his number cannot be bigger than 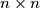 matrix
matrix 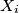 be the set of entries in row
be the set of entries in row  , and
, and 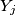 the set of entries in column
the set of entries in column  ,
, 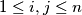 . We say that
. We say that 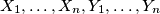 are distinct sets. Find the least integer
are distinct sets. Find the least integer 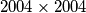 golden matrix with entries in the set
golden matrix with entries in the set 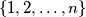 .
. 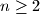 , let
, let  ,
, 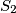 ,
,  ,
, 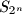 be
be 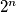 subsets of
subsets of 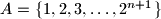 that satisfy the following property: There do not exist indices
that satisfy the following property: There do not exist indices  and
and  with
with 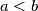 and elements
and elements  ,
,  ,
, 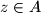 with
with 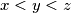 and
and 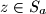 , and
, and 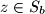 . Prove that at least one of the sets
. Prove that at least one of the sets 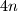 elements.
elements.