Slični zadaci
Let  be a convex polygon. Prove that there exists a convex hexagon that is contained in
be a convex polygon. Prove that there exists a convex hexagon that is contained in  and whose area is at least
and whose area is at least  of the area of the polygon
of the area of the polygon  .
.
Alternative version. Let be a convex polygon with
be a convex polygon with 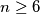 vertices. Prove that there exists a convex hexagon with
vertices. Prove that there exists a convex hexagon with
a) vertices on the sides of the polygon (or)
b) vertices among the vertices of the polygon
such that the area of the hexagon is at least of the area of the polygon.
of the area of the polygon.
I couldn't solve this one, partially because I'm not quite sure of the statements' meaning (a) or (b) :)
Obviously if a) is true then so is b).
 be a convex polygon. Prove that there exists a convex hexagon that is contained in
be a convex polygon. Prove that there exists a convex hexagon that is contained in  and whose area is at least
and whose area is at least  of the area of the polygon
of the area of the polygon  .
. Alternative version. Let
 be a convex polygon with
be a convex polygon with 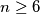 vertices. Prove that there exists a convex hexagon with
vertices. Prove that there exists a convex hexagon with a) vertices on the sides of the polygon (or)
b) vertices among the vertices of the polygon
such that the area of the hexagon is at least
 of the area of the polygon.
of the area of the polygon. I couldn't solve this one, partially because I'm not quite sure of the statements' meaning (a) or (b) :)
Obviously if a) is true then so is b).
In the Cartesian coordinate plane define the strips 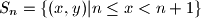 ,
, 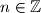 and color each strip black or white. Prove that any rectangle which is not a square can be placed in the plane so that its vertices have the same color.
and color each strip black or white. Prove that any rectangle which is not a square can be placed in the plane so that its vertices have the same color.
IMO Shortlist 2007 Problem C5 as it appears in the official booklet:In the Cartesian coordinate plane define the strips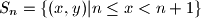 for every integer
for every integer  Assume each strip
Assume each strip 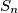 is colored either red or blue, and let
is colored either red or blue, and let  and
and  be two distinct positive integers. Prove that there exists a rectangle with side length
be two distinct positive integers. Prove that there exists a rectangle with side length  and
and  such that its vertices have the same color.
such that its vertices have the same color.
Edited by Orlando Döhring
Author: Radu Gologan and Dan Schwarz, Romania
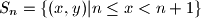 ,
, 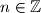 and color each strip black or white. Prove that any rectangle which is not a square can be placed in the plane so that its vertices have the same color.
and color each strip black or white. Prove that any rectangle which is not a square can be placed in the plane so that its vertices have the same color. IMO Shortlist 2007 Problem C5 as it appears in the official booklet:In the Cartesian coordinate plane define the strips
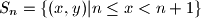 for every integer
for every integer  Assume each strip
Assume each strip 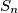 is colored either red or blue, and let
is colored either red or blue, and let  and
and  be two distinct positive integers. Prove that there exists a rectangle with side length
be two distinct positive integers. Prove that there exists a rectangle with side length  and
and  such that its vertices have the same color.
such that its vertices have the same color.Edited by Orlando Döhring
Author: Radu Gologan and Dan Schwarz, Romania
Let  and
and  be integers with
be integers with 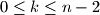 . Consider a set
. Consider a set  of
of  lines in the plane such that no two of them are parallel and no three have a common point. Denote by
lines in the plane such that no two of them are parallel and no three have a common point. Denote by  the set of intersections of lines in
the set of intersections of lines in  . Let
. Let  be a point in the plane not lying on any line of
be a point in the plane not lying on any line of  . A point
. A point 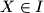 is colored red if the open line segment
is colored red if the open line segment 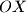 intersects at most
intersects at most  lines in
lines in  . Prove that
. Prove that  contains at least
contains at least 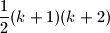 red points.
red points.
Proposed by Gerhard Woeginger, Netherlands
 and
and  be integers with
be integers with 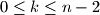 . Consider a set
. Consider a set  of
of  lines in the plane such that no two of them are parallel and no three have a common point. Denote by
lines in the plane such that no two of them are parallel and no three have a common point. Denote by  the set of intersections of lines in
the set of intersections of lines in  . Let
. Let  be a point in the plane not lying on any line of
be a point in the plane not lying on any line of  . A point
. A point 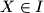 is colored red if the open line segment
is colored red if the open line segment 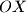 intersects at most
intersects at most  lines in
lines in  . Prove that
. Prove that  contains at least
contains at least 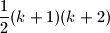 red points.
red points. Proposed by Gerhard Woeginger, Netherlands
On a 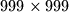 board a limp rook can move in the following way: From any square it can move to any of its adjacent squares, i.e. a square having a common side with it, and every move must be a turn, i.e. the directions of any two consecutive moves must be perpendicular. A non-intersecting route of the limp rook consists of a sequence of pairwise different squares that the limp rook can visit in that order by an admissible sequence of moves. Such a non-intersecting route is called cyclic, if the limp rook can, after reaching the last square of the route, move directly to the first square of the route and start over.
board a limp rook can move in the following way: From any square it can move to any of its adjacent squares, i.e. a square having a common side with it, and every move must be a turn, i.e. the directions of any two consecutive moves must be perpendicular. A non-intersecting route of the limp rook consists of a sequence of pairwise different squares that the limp rook can visit in that order by an admissible sequence of moves. Such a non-intersecting route is called cyclic, if the limp rook can, after reaching the last square of the route, move directly to the first square of the route and start over.
How many squares does the longest possible cyclic, non-intersecting route of a limp rook visit?
Proposed by Nikolay Beluhov, Bulgaria
 board a limp rook can move in the following way: From any square it can move to any of its adjacent squares, i.e. a square having a common side with it, and every move must be a turn, i.e. the directions of any two consecutive moves must be perpendicular. A non-intersecting route of the limp rook consists of a sequence of pairwise different squares that the limp rook can visit in that order by an admissible sequence of moves. Such a non-intersecting route is called cyclic, if the limp rook can, after reaching the last square of the route, move directly to the first square of the route and start over.
board a limp rook can move in the following way: From any square it can move to any of its adjacent squares, i.e. a square having a common side with it, and every move must be a turn, i.e. the directions of any two consecutive moves must be perpendicular. A non-intersecting route of the limp rook consists of a sequence of pairwise different squares that the limp rook can visit in that order by an admissible sequence of moves. Such a non-intersecting route is called cyclic, if the limp rook can, after reaching the last square of the route, move directly to the first square of the route and start over. How many squares does the longest possible cyclic, non-intersecting route of a limp rook visit?
Proposed by Nikolay Beluhov, Bulgaria
 Školjka
Školjka 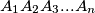 be a regular n-gon. Let
be a regular n-gon. Let  and
and 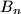 be the midpoints of its sides
be the midpoints of its sides 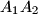 and
and 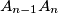 . Also, for every
. Also, for every 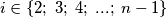 , let
, let  be the point of intersection of the lines
be the point of intersection of the lines 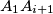 and
and 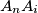 , and let
, and let 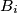 be the point of intersection of the angle bisector bisector of the angle
be the point of intersection of the angle bisector bisector of the angle 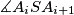 with the segment
with the segment 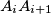 .
. 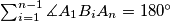 .
.  . Prove that there exists a point
. Prove that there exists a point 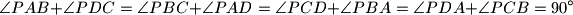
 and
and  are perpendicular.
are perpendicular.  satisfying
satisfying  we have
we have 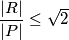 where
where 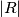 and
and 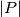 denote the area of the sets
denote the area of the sets