Slični zadaci
Let  be a positive integer. Prove that the number
be a positive integer. Prove that the number 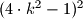 has a positive divisor of the form
has a positive divisor of the form 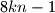 if and only if
if and only if  is even.
is even.
Actual IMO 2007 Problem, posed as question 5 in the contest, which was used as a lemma in the official solutions for problem N6 as shown above.
Author: Kevin Buzzard and Edward Crane, United Kingdom
 be a positive integer. Prove that the number
be a positive integer. Prove that the number 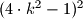 has a positive divisor of the form
has a positive divisor of the form 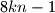 if and only if
if and only if  is even.
is even. Actual IMO 2007 Problem, posed as question 5 in the contest, which was used as a lemma in the official solutions for problem N6 as shown above.
Author: Kevin Buzzard and Edward Crane, United Kingdom
 Školjka
Školjka  such that
such that 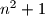 has a prime divisor greater than
has a prime divisor greater than 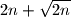 .
.  be a prime number. Prove that there exists a prime number
be a prime number. Prove that there exists a prime number  such that for every integer
such that for every integer 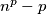 is not divisible by
is not divisible by 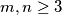 for which there exist infinitely many positive integers
for which there exist infinitely many positive integers  such that
such that 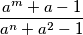 is itself an integer.
is itself an integer.  be positive integers and suppose that
be positive integers and suppose that  Prove that
Prove that  is not prime.
is not prime. 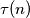 denote the number of its positive divisors (including 1 and itself). Determine all positive integers
denote the number of its positive divisors (including 1 and itself). Determine all positive integers  for which there exists a positive integer
for which there exists a positive integer 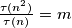 .
.