Let  be an odd prime and
be an odd prime and  a positive integer. In the coordinate plane, eight distinct points with integer coordinates lie on a circle with diameter of length
a positive integer. In the coordinate plane, eight distinct points with integer coordinates lie on a circle with diameter of length 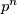 . Prove that there exists a triangle with vertices at three of the given points such that the squares of its side lengths are integers divisible by
. Prove that there exists a triangle with vertices at three of the given points such that the squares of its side lengths are integers divisible by 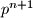 .
.
 be an odd prime and
be an odd prime and  a positive integer. In the coordinate plane, eight distinct points with integer coordinates lie on a circle with diameter of length
a positive integer. In the coordinate plane, eight distinct points with integer coordinates lie on a circle with diameter of length 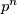 . Prove that there exists a triangle with vertices at three of the given points such that the squares of its side lengths are integers divisible by
. Prove that there exists a triangle with vertices at three of the given points such that the squares of its side lengths are integers divisible by 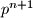 .
.  Školjka
Školjka