Find all functions
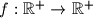
satisfying
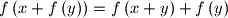
for all pairs of positive reals

and

. Here,
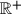
denotes the set of all positive reals.
Proposed by Paisan Nakmahachalasint, Thailand
%V0
Find all functions $f: \mathbb{R}^{ + }\to\mathbb{R}^{ + }$ satisfying $f\left(x + f\left(y\right)\right) = f\left(x + y\right) + f\left(y\right)$ for all pairs of positive reals $x$ and $y$. Here, $\mathbb{R}^{ + }$ denotes the set of all positive reals.
Proposed by Paisan Nakmahachalasint, Thailand