mozemo li iz svakog deveterclanog podskupa skupa prirodnih brojeva odabrati cetiri razlicita elementa

,

,

,

, tako da brojevi
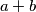
i
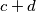
daju isti ostatak pri djeljenju s

?
%V0
mozemo li iz svakog deveterclanog podskupa skupa prirodnih brojeva odabrati cetiri razlicita elementa $a$, $b$, $c$, $d$, tako da brojevi $a + b$ i $c + d$ daju isti ostatak pri djeljenju s $20$?