Let

be a parallelogram. A variable line

through the vertex

intersects the rays

and
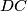
at the points

and

, respectively. Let

and

be the

-excenters of the triangles
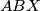
and
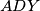
. Show that the angle
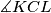
is independent of the line

.
%V0
Let $ABCD$ be a parallelogram. A variable line $g$ through the vertex $A$ intersects the rays $BC$ and $DC$ at the points $X$ and $Y$, respectively. Let $K$ and $L$ be the $A$-excenters of the triangles $ABX$ and $ADY$. Show that the angle $\measuredangle KCL$ is independent of the line $g$.