Let  be an acute-angled triangle with
be an acute-angled triangle with 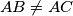 . Let
. Let  be the orthocenter of triangle
be the orthocenter of triangle  , and let
, and let  be the midpoint of the side
be the midpoint of the side  . Let
. Let  be a point on the side
be a point on the side  and
and  a point on the side
a point on the side  such that
such that 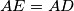 and the points
and the points  ,
,  ,
,  are on the same line. Prove that the line
are on the same line. Prove that the line 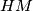 is perpendicular to the common chord of the circumscribed circles of triangle
is perpendicular to the common chord of the circumscribed circles of triangle  and triangle
and triangle 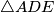 .
.
 be an acute-angled triangle with
be an acute-angled triangle with 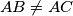 . Let
. Let  be the orthocenter of triangle
be the orthocenter of triangle  , and let
, and let  be the midpoint of the side
be the midpoint of the side  . Let
. Let  be a point on the side
be a point on the side  and
and  a point on the side
a point on the side  such that
such that 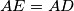 and the points
and the points  ,
,  ,
,  are on the same line. Prove that the line
are on the same line. Prove that the line 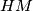 is perpendicular to the common chord of the circumscribed circles of triangle
is perpendicular to the common chord of the circumscribed circles of triangle  and triangle
and triangle 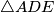 .
.  Školjka
Školjka