In an acute triangle

, let

,

,

be the feet of the perpendiculars from the points

,

,

to the lines

,

,

, respectively, and let

,

,

be the feet of the perpendiculars from the points

,

,

to the lines

,
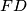
,
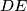
, respectively.
Prove that
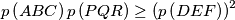
, where
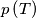
denotes the perimeter of triangle

.
%V0
In an acute triangle $ABC$, let $D$, $E$, $F$ be the feet of the perpendiculars from the points $A$, $B$, $C$ to the lines $BC$, $CA$, $AB$, respectively, and let $P$, $Q$, $R$ be the feet of the perpendiculars from the points $A$, $B$, $C$ to the lines $EF$, $FD$, $DE$, respectively.
Prove that $p\left(ABC\right)p\left(PQR\right) \ge \left(p\left(DEF\right)\right)^{2}$, where $p\left(T\right)$ denotes the perimeter of triangle $T$ .