Let
be triangle with incenter
. A point
in the interior of the triangle satisfies
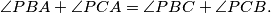
Show that
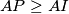
, and that equality holds if and only if
.
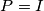
%V0
Let $ABC$ be triangle with incenter $I$. A point $P$ in the interior of the triangle satisfies $$\angle PBA+\angle PCA = \angle PBC+\angle PCB.$$ Show that $AP \geq AI$, and that equality holds if and only if $P=I$.
Školjka