Let

be a trapezoid with parallel sides
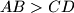
. Points

and

lie on the line segments

and

, respectively, so that
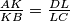
. Suppose that there are points

and

on the line segment
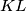
satisfying
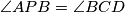
and
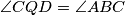
. Prove that the points

,

,

and

are concylic.
%V0
Let $ABC$ be a trapezoid with parallel sides $AB > CD$. Points $K$ and $L$ lie on the line segments $AB$ and $CD$, respectively, so that $\frac {AK}{KB} = \frac {DL}{LC}$. Suppose that there are points $P$ and $Q$ on the line segment $KL$ satisfying $\angle{APB} = \angle{BCD}$ and $\angle{CQD} = \angle{ABC}$. Prove that the points $P$, $Q$, $B$ and $C$ are concylic.