IMO Shortlist 2006 problem C4
Kvaliteta:
Avg: 3,0Težina:
Avg: 7,0 A cake has the form of an  x
x  square composed of
square composed of 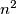 unit squares. Strawberries lie on some of the unit squares so that each row or column contains exactly one strawberry; call this arrangement
unit squares. Strawberries lie on some of the unit squares so that each row or column contains exactly one strawberry; call this arrangement  . Let
. Let  be another such arrangement. Suppose that every grid rectangle with one vertex at the top left corner of the cake contains no fewer strawberries of arrangement
be another such arrangement. Suppose that every grid rectangle with one vertex at the top left corner of the cake contains no fewer strawberries of arrangement  than of arrangement
than of arrangement  .
.
Prove that arrangement can be obtained from
can be obtained from  by performing a number of switches, defined as follows: A switch consists in selecting a grid rectangle with only two strawberries, situated at its top right corner and bottom left corner, and moving these two strawberries to the other two corners of that rectangle.
by performing a number of switches, defined as follows: A switch consists in selecting a grid rectangle with only two strawberries, situated at its top right corner and bottom left corner, and moving these two strawberries to the other two corners of that rectangle.
 x
x  square composed of
square composed of 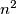 unit squares. Strawberries lie on some of the unit squares so that each row or column contains exactly one strawberry; call this arrangement
unit squares. Strawberries lie on some of the unit squares so that each row or column contains exactly one strawberry; call this arrangement  . Let
. Let  be another such arrangement. Suppose that every grid rectangle with one vertex at the top left corner of the cake contains no fewer strawberries of arrangement
be another such arrangement. Suppose that every grid rectangle with one vertex at the top left corner of the cake contains no fewer strawberries of arrangement  than of arrangement
than of arrangement  .
. Prove that arrangement
 can be obtained from
can be obtained from  by performing a number of switches, defined as follows: A switch consists in selecting a grid rectangle with only two strawberries, situated at its top right corner and bottom left corner, and moving these two strawberries to the other two corners of that rectangle.
by performing a number of switches, defined as follows: A switch consists in selecting a grid rectangle with only two strawberries, situated at its top right corner and bottom left corner, and moving these two strawberries to the other two corners of that rectangle. Izvor: Međunarodna matematička olimpijada, shortlist 2006
 Školjka
Školjka 
