Consider a convex pentagon
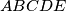
such that
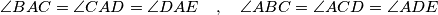
Let
be the point of intersection of the lines
and
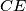
. Prove that the line
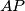
passes through the midpoint of the side
.
%V0
Consider a convex pentagon $ABCDE$ such that
$$\angle BAC = \angle CAD = \angle DAE\ \ \ ,\ \ \ \angle ABC = \angle ACD = \angle ADE$$
Let $P$ be the point of intersection of the lines $BD$ and $CE$. Prove that the line $AP$ passes through the midpoint of the side $CD$.
Školjka