Slični zadaci
An acute triangle  is given. Points
is given. Points  and
and  are taken on the side
are taken on the side  (with
(with  between
between  and
and  ),
),  and
and  on the side
on the side  (with
(with  between
between  and
and  ), and
), and  and
and 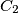 on the side
on the side  (with
(with 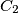 between
between  and
and  ) so that
) so that
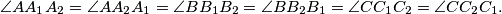
The lines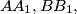 and
and 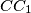 bound a triangle, and the lines
bound a triangle, and the lines 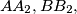 and
and 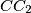 bound a second triangle. Prove that all six vertices of these two triangles lie on a single circle.
bound a second triangle. Prove that all six vertices of these two triangles lie on a single circle.
 is given. Points
is given. Points  and
and  are taken on the side
are taken on the side  (with
(with  between
between  and
and  ),
),  and
and  on the side
on the side  (with
(with  between
between  and
and  ), and
), and  and
and 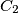 on the side
on the side  (with
(with 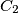 between
between  and
and  ) so that
) so that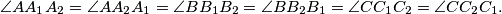
The lines
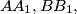 and
and 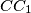 bound a triangle, and the lines
bound a triangle, and the lines 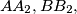 and
and 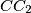 bound a second triangle. Prove that all six vertices of these two triangles lie on a single circle.
bound a second triangle. Prove that all six vertices of these two triangles lie on a single circle.  Školjka
Školjka 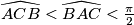 . Let
. Let  be a point of
be a point of ![[AC]](/media/m/c/7/4/c741f6e67c75b27db5e363fbcf5393c6.png) such that
such that 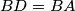 . The incircle of
. The incircle of ![[AB]](/media/m/1/0/6/10652e809a6cb10509d19772365232e2.png) at
at  and
and  . Let
. Let 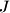 be the center of the incircle of
be the center of the incircle of  . Prove that
. Prove that 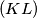 intersects
intersects ![[AJ]](/media/m/4/d/3/4d35637bd1d22b6a0da26de27970690f.png) at its middle.
at its middle.  be points on the side
be points on the side 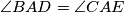 . If
. If  and
and  are, respectively, the points of tangency of the incircles of the triangles
are, respectively, the points of tangency of the incircles of the triangles 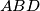 and
and 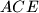 with the line
with the line 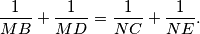
 touches the sides
touches the sides  ,
,  respectively.
respectively.  is a point inside triangle of
is a point inside triangle of  touches
touches 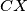 and
and 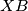 at
at  and
and  respectively.
respectively. 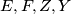 are concyclic.
are concyclic.  and
and 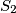 intersect at points
intersect at points  and
and  . Distinct points
. Distinct points 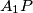 and
and 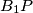 meet
meet 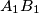 and
and 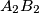 meet at
meet at 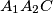 all lie on one fixed circle.
all lie on one fixed circle.  and
and 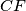 are altitudes. Two circles passing through the point
are altitudes. Two circles passing through the point  and tangent to the line
and tangent to the line 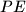 and
and 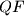 intersect on the circumcircle of triangle
intersect on the circumcircle of triangle 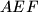 .
. be the point where the lines
be the point where the lines 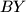 and
and 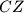 meet, and let
meet, and let  and
and  be points such that the two quadrilaterals
be points such that the two quadrilaterals 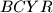 and
and 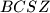 are parallelogram.
are parallelogram.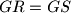 .
.