In triangle

, let
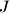
be the center of the excircle tangent to side

at
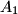
and to the extensions of the sides

and

at
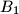
and
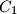
respectively. Suppose that the lines
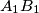
and

are perpendicular and intersect at

. Let

be the foot of the perpendicular from
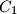
to line
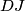
. Determine the angles
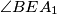
and
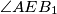
.
%V0
In triangle $ABC$, let $J$ be the center of the excircle tangent to side $BC$ at $A_{1}$ and to the extensions of the sides $AC$ and $AB$ at $B_{1}$ and $C_{1}$ respectively. Suppose that the lines $A_{1}B_{1}$ and $AB$ are perpendicular and intersect at $D$. Let $E$ be the foot of the perpendicular from $C_{1}$ to line $DJ$. Determine the angles $\angle{BEA_{1}}$ and $\angle{AEB_{1}}$.