Slični zadaci
Denote by 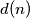 the number of divisors of the positive integer
the number of divisors of the positive integer  . A positive integer
. A positive integer  is called highly divisible if
is called highly divisible if 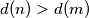 for all positive integers
for all positive integers 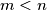 .
.
Two highly divisible integers and
and  with
with 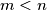 are called consecutive if there exists no highly divisible integer
are called consecutive if there exists no highly divisible integer  satisfying
satisfying 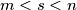 .
.
(a) Show that there are only finitely many pairs of consecutive highly divisible
integers of the form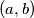 with
with 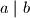 .
.
(b) Show that for every prime number there exist infinitely many positive highly divisible integers
there exist infinitely many positive highly divisible integers  such that
such that 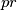 is also highly divisible.
is also highly divisible.
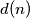 the number of divisors of the positive integer
the number of divisors of the positive integer  . A positive integer
. A positive integer  is called highly divisible if
is called highly divisible if 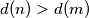 for all positive integers
for all positive integers 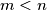 .
. Two highly divisible integers
 and
and  with
with 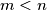 are called consecutive if there exists no highly divisible integer
are called consecutive if there exists no highly divisible integer  satisfying
satisfying 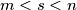 .
. (a) Show that there are only finitely many pairs of consecutive highly divisible
integers of the form
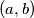 with
with 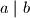 .
. (b) Show that for every prime number
 there exist infinitely many positive highly divisible integers
there exist infinitely many positive highly divisible integers  such that
such that 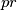 is also highly divisible.
is also highly divisible. We define a sequence 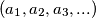 by setting
by setting
![a_{n} = \frac {1}{n}\left(\left[\frac {n}{1}\right] + \left[\frac {n}{2}\right] + \cdots + \left[\frac {n}{n}\right]\right)](/media/m/0/f/c/0fcd7236589e4454f518b8d8aa9fe147.png)
for every positive integer . Hereby, for every real
. Hereby, for every real  , we denote by
, we denote by ![\left[x\right]](/media/m/3/6/9/3697c66f8530757a1166f24a1fd325e6.png) the integral part of
the integral part of  (this is the greatest integer which is
(this is the greatest integer which is 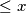 ).
).
a) Prove that there is an infinite number of positive integers such that
such that 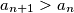 .
.
b) Prove that there is an infinite number of positive integers such that
such that 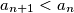 .
.
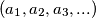 by setting
by setting ![a_{n} = \frac {1}{n}\left(\left[\frac {n}{1}\right] + \left[\frac {n}{2}\right] + \cdots + \left[\frac {n}{n}\right]\right)](/media/m/0/f/c/0fcd7236589e4454f518b8d8aa9fe147.png)
for every positive integer
 . Hereby, for every real
. Hereby, for every real  , we denote by
, we denote by ![\left[x\right]](/media/m/3/6/9/3697c66f8530757a1166f24a1fd325e6.png) the integral part of
the integral part of  (this is the greatest integer which is
(this is the greatest integer which is 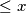 ).
). a) Prove that there is an infinite number of positive integers
 such that
such that 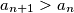 .
. b) Prove that there is an infinite number of positive integers
 such that
such that 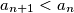 .
.  Školjka
Školjka 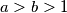 be relatively prime positive integers. Define the weight of an integer
be relatively prime positive integers. Define the weight of an integer  , denoted by
, denoted by 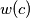 to be the minimal possible value of
to be the minimal possible value of 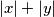 taken over all pairs of integers
taken over all pairs of integers  such that
such that 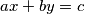 . An integer
. An integer 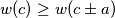 and
and 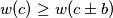 . Find all local champions and determine their number.
. Find all local champions and determine their number.  ,
,  be positive integers such that
be positive integers such that 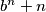 is a multiple of
is a multiple of 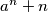 for all positive integers
for all positive integers 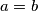 .
. 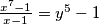 doesn't have integer solutions!
doesn't have integer solutions! 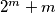 .
.  be a positive integer. Show that if there exists a sequence
be a positive integer. Show that if there exists a sequence 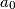 ,
,  , ... of integers satisfying the condition
, ... of integers satisfying the condition 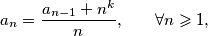 then
then 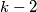 is divisible by
is divisible by  .
.