Let

be a positive integer, and let

and

be a positive real number such that
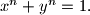
Prove that
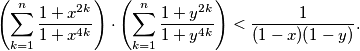
Author: unknown author, Estonia
%V0
Let $n$ be a positive integer, and let $x$ and $y$ be a positive real number such that $x^n + y^n = 1.$ Prove that $$
\left(\sum^n_{k = 1} \frac {1 + x^{2k}}{1 + x^{4k}} \right) \cdot \left( \sum^n_{k = 1} \frac {1 + y^{2k}}{1 + y^{4k}} \right) < \frac{1}{(1 - x)(1 - y)} \text{.}$$
Author: unknown author, Estonia