Let
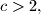
and let
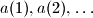
be a sequence of nonnegative real numbers such that
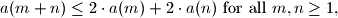
and
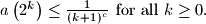
Prove that the sequence
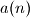
is bounded.
Author: Vjekoslav Kovač, Croatia
%V0
Let $c > 2,$ and let $a(1), a(2), \ldots$ be a sequence of nonnegative real numbers such that
$$a(m + n) \leq 2 \cdot a(m) + 2 \cdot a(n) \text{ for all } m,n \geq 1,$$
and $a\left(2^k \right) \leq \frac {1}{(k + 1)^c} \text{ for all } k \geq 0.$ Prove that the sequence $a(n)$ is bounded.
Author: Vjekoslav Kovač, Croatia