Let
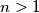
be an integer. Find all sequences
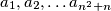
satisfying the following conditions:
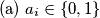
for all
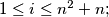
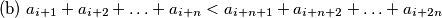
for all
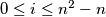
Author: unknown author, Serbia
%V0
Let $n > 1$ be an integer. Find all sequences $a_1, a_2, \ldots a_{n^2 + n}$ satisfying the following conditions:
$\text{ (a) } a_i \in \left\{0,1\right\}$ for all $1 \leq i \leq n^2 + n;$
$\text{ (b) } a_{i + 1} + a_{i + 2} + \ldots + a_{i + n} < a_{i + n + 1} + a_{i + n + 2} + \ldots + a_{i + 2n}$ for all $0 \leq i \leq n^2 - n$
Author: unknown author, Serbia