Slični zadaci
A tetrahedron is called a MEMO-tetrahedron if all six sidelengths are different positive integers where one of them is  and one of them is
and one of them is  . Let
. Let 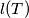 be the sum of the sidelengths of the tetrahedron
be the sum of the sidelengths of the tetrahedron  .
.
(a) Find all positive integers so that there exists a MEMO-Tetrahedron
so that there exists a MEMO-Tetrahedron  with
with 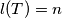 .
.
(b) How many pairwise non-congruent MEMO-tetrahedrons satisfying
satisfying 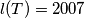 exist? Two tetrahedrons are said to be non-congruent if one cannot be obtained from the other by a composition of reflections in planes, translations and rotations. (It is not neccessary to prove that the tetrahedrons are not degenerate, i.e. that they have a positive volume).
exist? Two tetrahedrons are said to be non-congruent if one cannot be obtained from the other by a composition of reflections in planes, translations and rotations. (It is not neccessary to prove that the tetrahedrons are not degenerate, i.e. that they have a positive volume).
 and one of them is
and one of them is  . Let
. Let 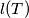 be the sum of the sidelengths of the tetrahedron
be the sum of the sidelengths of the tetrahedron  .
. (a) Find all positive integers
 so that there exists a MEMO-Tetrahedron
so that there exists a MEMO-Tetrahedron  with
with 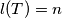 .
. (b) How many pairwise non-congruent MEMO-tetrahedrons
 satisfying
satisfying 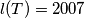 exist? Two tetrahedrons are said to be non-congruent if one cannot be obtained from the other by a composition of reflections in planes, translations and rotations. (It is not neccessary to prove that the tetrahedrons are not degenerate, i.e. that they have a positive volume).
exist? Two tetrahedrons are said to be non-congruent if one cannot be obtained from the other by a composition of reflections in planes, translations and rotations. (It is not neccessary to prove that the tetrahedrons are not degenerate, i.e. that they have a positive volume). For an integer 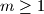 , we consider partitions of a
, we consider partitions of a  chessboard into rectangles consisting of cells of chessboard, in which each of the
chessboard into rectangles consisting of cells of chessboard, in which each of the 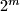 cells along one diagonal forms a separate rectangle of side length
cells along one diagonal forms a separate rectangle of side length  . Determine the smallest possible sum of rectangle perimeters in such a partition.
. Determine the smallest possible sum of rectangle perimeters in such a partition.
Proposed by Gerhard Woeginger, Netherlands
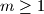 , we consider partitions of a
, we consider partitions of a  chessboard into rectangles consisting of cells of chessboard, in which each of the
chessboard into rectangles consisting of cells of chessboard, in which each of the 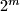 cells along one diagonal forms a separate rectangle of side length
cells along one diagonal forms a separate rectangle of side length  . Determine the smallest possible sum of rectangle perimeters in such a partition.
. Determine the smallest possible sum of rectangle perimeters in such a partition.Proposed by Gerhard Woeginger, Netherlands
In the Cartesian coordinate plane define the strips 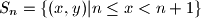 ,
, 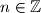 and color each strip black or white. Prove that any rectangle which is not a square can be placed in the plane so that its vertices have the same color.
and color each strip black or white. Prove that any rectangle which is not a square can be placed in the plane so that its vertices have the same color.
IMO Shortlist 2007 Problem C5 as it appears in the official booklet:In the Cartesian coordinate plane define the strips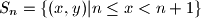 for every integer
for every integer  Assume each strip
Assume each strip 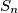 is colored either red or blue, and let
is colored either red or blue, and let  and
and  be two distinct positive integers. Prove that there exists a rectangle with side length
be two distinct positive integers. Prove that there exists a rectangle with side length  and
and  such that its vertices have the same color.
such that its vertices have the same color.
Edited by Orlando Döhring
Author: Radu Gologan and Dan Schwarz, Romania
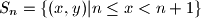 ,
, 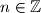 and color each strip black or white. Prove that any rectangle which is not a square can be placed in the plane so that its vertices have the same color.
and color each strip black or white. Prove that any rectangle which is not a square can be placed in the plane so that its vertices have the same color. IMO Shortlist 2007 Problem C5 as it appears in the official booklet:In the Cartesian coordinate plane define the strips
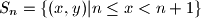 for every integer
for every integer  Assume each strip
Assume each strip 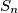 is colored either red or blue, and let
is colored either red or blue, and let  and
and  be two distinct positive integers. Prove that there exists a rectangle with side length
be two distinct positive integers. Prove that there exists a rectangle with side length  and
and  such that its vertices have the same color.
such that its vertices have the same color.Edited by Orlando Döhring
Author: Radu Gologan and Dan Schwarz, Romania
A rectangle  is partitioned in several (
is partitioned in several (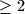 ) rectangles with sides parallel to those of
) rectangles with sides parallel to those of  . Given that any line parallel to one of the sides of
. Given that any line parallel to one of the sides of  , and having common points with the interior of
, and having common points with the interior of  , also has common interior points with the interior of at least one rectangle of the partition; prove that there is at least one rectangle of the partition having no common points with
, also has common interior points with the interior of at least one rectangle of the partition; prove that there is at least one rectangle of the partition having no common points with  's boundary.
's boundary.
Author: unknown author, Japan
 is partitioned in several (
is partitioned in several (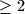 ) rectangles with sides parallel to those of
) rectangles with sides parallel to those of  . Given that any line parallel to one of the sides of
. Given that any line parallel to one of the sides of  , and having common points with the interior of
, and having common points with the interior of  , also has common interior points with the interior of at least one rectangle of the partition; prove that there is at least one rectangle of the partition having no common points with
, also has common interior points with the interior of at least one rectangle of the partition; prove that there is at least one rectangle of the partition having no common points with  's boundary.
's boundary. Author: unknown author, Japan
A circle  bisects a circle
bisects a circle  if it cuts
if it cuts  at opposite ends of a diameter.
at opposite ends of a diameter.  ,
,  ,
, are circles with distinct centers
are circles with distinct centers  (respectively).
(respectively).
Show that are collinear iff there is no unique circle
are collinear iff there is no unique circle  which bisects each of
which bisects each of  ,
,  ,
, . Show that if there is more than one circle
. Show that if there is more than one circle  which bisects each of
which bisects each of  ,
,  ,
, , then all such circles pass through two fixed points. Find these points.
, then all such circles pass through two fixed points. Find these points.
Original Statement:
A circle is said to cut a circle
is said to cut a circle 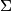 diametrically if and only if their common chord is a diameter of
diametrically if and only if their common chord is a diameter of 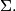
Let be three circles with distinct centres
be three circles with distinct centres  respectively. Prove that
respectively. Prove that  are collinear if and only if there is no unique circle
are collinear if and only if there is no unique circle  which cuts each of
which cuts each of  diametrically. Prove further that if there exists more than one circle
diametrically. Prove further that if there exists more than one circle  which cuts each
which cuts each  diametrically, then all such circles
diametrically, then all such circles  pass through two fixed points. Locate these points in relation to the circles
pass through two fixed points. Locate these points in relation to the circles 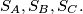
 bisects a circle
bisects a circle  if it cuts
if it cuts  at opposite ends of a diameter.
at opposite ends of a diameter.  ,
,  ,
, are circles with distinct centers
are circles with distinct centers  (respectively).
(respectively). Show that
 are collinear iff there is no unique circle
are collinear iff there is no unique circle  which bisects each of
which bisects each of  ,
,  ,
, . Show that if there is more than one circle
. Show that if there is more than one circle  which bisects each of
which bisects each of  ,
,  ,
, , then all such circles pass through two fixed points. Find these points.
, then all such circles pass through two fixed points. Find these points. Original Statement:
A circle
 is said to cut a circle
is said to cut a circle 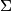 diametrically if and only if their common chord is a diameter of
diametrically if and only if their common chord is a diameter of 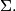
Let
 be three circles with distinct centres
be three circles with distinct centres  respectively. Prove that
respectively. Prove that  are collinear if and only if there is no unique circle
are collinear if and only if there is no unique circle  which cuts each of
which cuts each of  diametrically. Prove further that if there exists more than one circle
diametrically. Prove further that if there exists more than one circle  which cuts each
which cuts each  diametrically, then all such circles
diametrically, then all such circles  pass through two fixed points. Locate these points in relation to the circles
pass through two fixed points. Locate these points in relation to the circles 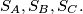
 Školjka
Školjka  intersect at point
intersect at point  . Point
. Point  lies between the parallel lines
lies between the parallel lines  and
and  such that
such that 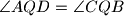 , and line
, and line  separates points
separates points 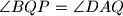 .
.  and
and  meet at
meet at  and the lines
and the lines  . The midpoints of
. The midpoints of  and
and  and
and  , respectively. Show that
, respectively. Show that  is tangent at
is tangent at