(i) If

,

and

are three real numbers, all different from

, such that
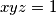
, then prove that
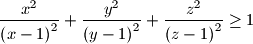
.
(With the
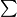
sign for cyclic summation, this inequality could be rewritten as
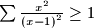
.)
(ii) Prove that equality is achieved for infinitely many triples of rational numbers

,

and

.
Author: Walther Janous, Austria
%V0
(i) If $x$, $y$ and $z$ are three real numbers, all different from $1$, such that $xyz = 1$, then prove that
$$\frac {x^{2}}{\left(x - 1\right)^{2}} + \frac {y^{2}}{\left(y - 1\right)^{2}} + \frac {z^{2}}{\left(z - 1\right)^{2}} \geq 1$$.
(With the $\sum$ sign for cyclic summation, this inequality could be rewritten as $\sum \frac {x^{2}}{\left(x - 1\right)^{2}} \geq 1$.)
(ii) Prove that equality is achieved for infinitely many triples of rational numbers $x$, $y$ and $z$.
Author: Walther Janous, Austria