Let
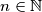
and
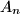
set of all permutations
of the set
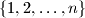
for which
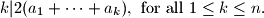
Find the number of elements of the set
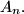
%V0
Let $n \in \mathbb N$ and $A_n$ set of all permutations $(a_1, \ldots, a_n)$ of the set $\{1, 2, \ldots , n\}$ for which
$$k|2(a_1 + \cdots+ a_k), \text{ for all } 1 \leq k \leq n.$$
Find the number of elements of the set $A_n.$
Školjka