Let  and
and  be positive integers with
be positive integers with 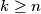 and
and  an even number. Let
an even number. Let  lamps labelled
lamps labelled  ,
,  , ...,
, ...,  be given, each of which can be either on or off. Initially all the lamps are off. We consider sequences of steps: at each step one of the lamps is switched (from on to off or from off to on).
be given, each of which can be either on or off. Initially all the lamps are off. We consider sequences of steps: at each step one of the lamps is switched (from on to off or from off to on).
Let be the number of such sequences consisting of
be the number of such sequences consisting of  steps and resulting in the state where lamps
steps and resulting in the state where lamps  through
through  are all on, and lamps
are all on, and lamps  through
through  are all off.
are all off.
Let be number of such sequences consisting of
be number of such sequences consisting of  steps, resulting in the state where lamps
steps, resulting in the state where lamps  through
through  are all on, and lamps
are all on, and lamps  through
through  are all off, but where none of the lamps
are all off, but where none of the lamps  through
through  is ever switched on.
is ever switched on.
Determine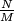 .
.
Author: Bruno Le Floch and Ilia Smilga, France
 and
and  be positive integers with
be positive integers with 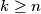 and
and  an even number. Let
an even number. Let  lamps labelled
lamps labelled  ,
,  , ...,
, ...,  be given, each of which can be either on or off. Initially all the lamps are off. We consider sequences of steps: at each step one of the lamps is switched (from on to off or from off to on).
be given, each of which can be either on or off. Initially all the lamps are off. We consider sequences of steps: at each step one of the lamps is switched (from on to off or from off to on). Let
 be the number of such sequences consisting of
be the number of such sequences consisting of  steps and resulting in the state where lamps
steps and resulting in the state where lamps  through
through  are all on, and lamps
are all on, and lamps  through
through  are all off.
are all off. Let
 be number of such sequences consisting of
be number of such sequences consisting of  steps, resulting in the state where lamps
steps, resulting in the state where lamps  through
through  are all on, and lamps
are all on, and lamps  through
through  are all off, but where none of the lamps
are all off, but where none of the lamps  through
through  is ever switched on.
is ever switched on. Determine
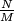 .
. Author: Bruno Le Floch and Ilia Smilga, France
 Školjka
Školjka