Slični zadaci
Na nekom turističkom putovanju bilo je ukupno  turista. Utvrđeno je da su bilo koja dvojica od njih bili međusobno "na ti" ili "na vi" ili uopće nisu razgovarali. Dokažite da među tih
turista. Utvrđeno je da su bilo koja dvojica od njih bili međusobno "na ti" ili "na vi" ili uopće nisu razgovarali. Dokažite da među tih  ljudi postoje bar trojica koji su međusobno bili "na ti" ili bar trojica koji su međusobno bili "na vi" ili bar trojica koji međusobno nisu razgovarali.
ljudi postoje bar trojica koji su međusobno bili "na ti" ili bar trojica koji su međusobno bili "na vi" ili bar trojica koji međusobno nisu razgovarali.
 turista. Utvrđeno je da su bilo koja dvojica od njih bili međusobno "na ti" ili "na vi" ili uopće nisu razgovarali. Dokažite da među tih
turista. Utvrđeno je da su bilo koja dvojica od njih bili međusobno "na ti" ili "na vi" ili uopće nisu razgovarali. Dokažite da među tih  ljudi postoje bar trojica koji su međusobno bili "na ti" ili bar trojica koji su međusobno bili "na vi" ili bar trojica koji međusobno nisu razgovarali.
ljudi postoje bar trojica koji su međusobno bili "na ti" ili bar trojica koji su međusobno bili "na vi" ili bar trojica koji međusobno nisu razgovarali. Dan je 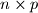 pravokutnik podijeljen na
pravokutnik podijeljen na 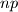 jedinicnih kvadratica. Na pocetku je
jedinicnih kvadratica. Na pocetku je  kvadratica crnih, a svi ostali su bijeli. Dozvoljena je sljedeca operacija: bijeli kvadratic koji ima zajednicki brid s barem dva crna kvadratica, moze postati crni. Nadi najmanji moguci
kvadratica crnih, a svi ostali su bijeli. Dozvoljena je sljedeca operacija: bijeli kvadratic koji ima zajednicki brid s barem dva crna kvadratica, moze postati crni. Nadi najmanji moguci  takav da postoji polazna pozicija iz koje, primjenom ovih operacija, mogu svi kvadratici postati crni.
takav da postoji polazna pozicija iz koje, primjenom ovih operacija, mogu svi kvadratici postati crni.
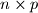 pravokutnik podijeljen na
pravokutnik podijeljen na 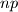 jedinicnih kvadratica. Na pocetku je
jedinicnih kvadratica. Na pocetku je  kvadratica crnih, a svi ostali su bijeli. Dozvoljena je sljedeca operacija: bijeli kvadratic koji ima zajednicki brid s barem dva crna kvadratica, moze postati crni. Nadi najmanji moguci
kvadratica crnih, a svi ostali su bijeli. Dozvoljena je sljedeca operacija: bijeli kvadratic koji ima zajednicki brid s barem dva crna kvadratica, moze postati crni. Nadi najmanji moguci  takav da postoji polazna pozicija iz koje, primjenom ovih operacija, mogu svi kvadratici postati crni.
takav da postoji polazna pozicija iz koje, primjenom ovih operacija, mogu svi kvadratici postati crni. U jednom vrhu kocke nalaze se dva pauka, a u suprotnom vrhu muha. Pauci i muha kreću se isključivo po bridovima kocke jednakim konstantnim brzinama. U svakom trenutku paucima je poznata pozicija muhe i muhi je poznata pozicija pauka. Dokaži da pauci mogu uhvatiti muhu. Smatra se da je muha uhvaćena ako se nađe u istoj točki kao i jedan od paukova.
 Školjka
Školjka 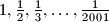 . Učenik odabire dva broja s ploče, recimo
. Učenik odabire dva broja s ploče, recimo  i
i  , te izračuna broj
, te izračuna broj 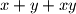 , rezultat zapiše na ploču, a
, rezultat zapiše na ploču, a 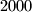 puta.
puta.  ,
,  ,
,  ,
,  , tako da brojevi
, tako da brojevi 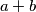 i
i 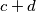 daju isti ostatak pri djeljenju s
daju isti ostatak pri djeljenju s  ?
?  sadrži
sadrži  prirodnih brojeva, od kojih je svaki manji od
prirodnih brojeva, od kojih je svaki manji od 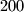 . Pokažite da postoji neprazan podskup
. Pokažite da postoji neprazan podskup  od
od 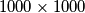 obojano je crnom ili bijelom bojom. Ukupan broj crnih polja na ploči je za
obojano je crnom ili bijelom bojom. Ukupan broj crnih polja na ploči je za 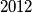 veći od ukupnog broja bijelih polja. Dokaži da postoji kvadrat
veći od ukupnog broja bijelih polja. Dokaži da postoji kvadrat 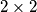 koji sadrži tri polja jedne boje i jedno polje druge boje.
koji sadrži tri polja jedne boje i jedno polje druge boje.