Let

,

,

be positive real numbers such that
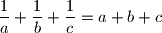
. Prove that:
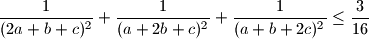
Proposed by Juhan Aru, Estonia
%V0
Let $a$, $b$, $c$ be positive real numbers such that $\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} = a+b+c$. Prove that:
$$\frac{1}{(2a+b+c)^2}+\frac{1}{(a+2b+c)^2}+\frac{1}{(a+b+2c)^2}\leq \frac{3}{16}$$
Proposed by Juhan Aru, Estonia