Slični zadaci
Let  be the set of all pairs
be the set of all pairs 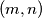 of relatively prime positive integers
of relatively prime positive integers 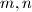 with
with  even and
even and 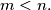 For
For 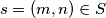 write
write 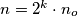 where
where 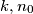 are positive integers with
are positive integers with 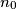 odd and define
odd and define 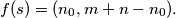 Prove that
Prove that  is a function from
is a function from  to
to  and that for each
and that for each 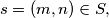 there exists a positive integer
there exists a positive integer 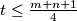 such that
such that 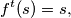 where
where 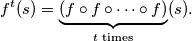
If is a prime number which does not divide
is a prime number which does not divide 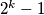 for
for 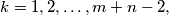 prove that the smallest value
prove that the smallest value  which satisfies the above conditions is
which satisfies the above conditions is ![\left [\frac{m+n+1}{4} \right ]](/media/m/8/7/8/878d7261cbd40fe8c838d36d2b94fea7.png) where
where ![\left[ x \right]](/media/m/8/4/7/847a3b7449538c2b99179a2953e7f9e0.png) denotes the greatest integer
denotes the greatest integer 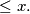
 be the set of all pairs
be the set of all pairs 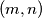 of relatively prime positive integers
of relatively prime positive integers 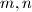 with
with  even and
even and 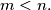 For
For 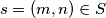 write
write 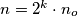 where
where 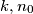 are positive integers with
are positive integers with 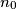 odd and define
odd and define 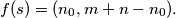 Prove that
Prove that  is a function from
is a function from  to
to  and that for each
and that for each 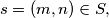 there exists a positive integer
there exists a positive integer 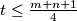 such that
such that 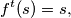 where
where 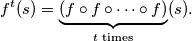
If
 is a prime number which does not divide
is a prime number which does not divide 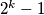 for
for 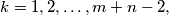 prove that the smallest value
prove that the smallest value  which satisfies the above conditions is
which satisfies the above conditions is ![\left [\frac{m+n+1}{4} \right ]](/media/m/8/7/8/878d7261cbd40fe8c838d36d2b94fea7.png) where
where ![\left[ x \right]](/media/m/8/4/7/847a3b7449538c2b99179a2953e7f9e0.png) denotes the greatest integer
denotes the greatest integer 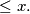
 Školjka
Školjka  divides
divides 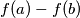 for all distinct positive integers
for all distinct positive integers  ,
,  . Prove that there exist infinitely many primes
. Prove that there exist infinitely many primes  such that
such that 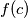 for some positive integer
for some positive integer  .
. is defined on the set of nonnegative integers and takes nonnegative integer values satisfying the following conditions: for every
is defined on the set of nonnegative integers and takes nonnegative integer values satisfying the following conditions: for every 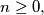
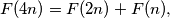
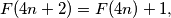
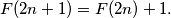
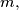 the number of integers
the number of integers 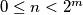 and
and 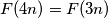 is
is 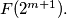
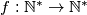 satisfying
satisfying 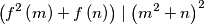
 and
and 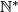 stands for the set of all positive integers:
stands for the set of all positive integers: 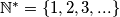 .
. 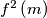 , we mean
, we mean 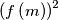 (and not
(and not 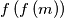 ).
). 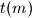 the unique number in
the unique number in 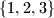 such that
such that 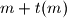 is a multiple of
is a multiple of  . A function
. A function 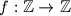 satisfies
satisfies 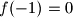 ,
, 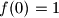 ,
, 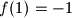 and
and 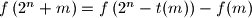 for all integers
for all integers 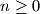 with
with  . Prove that
. Prove that 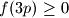 holds for all integers
holds for all integers 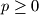 .
. 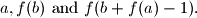
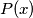 be a non-constant polynomial with integer coefficients. Prove that there is no function
be a non-constant polynomial with integer coefficients. Prove that there is no function  from the set of integers into the set of integers such that the number of integers
from the set of integers into the set of integers such that the number of integers  with
with 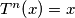 is equal to
is equal to 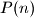 for every
for every 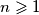 , where
, where 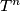 denotes the
denotes the