Slični zadaci
The sequence 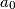 ,
,  ,
, 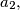
 is defined as follows:
is defined as follows: 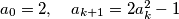 for
for 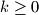 . Prove that if an odd prime
. Prove that if an odd prime  divides
divides  , then
, then 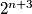 divides
divides 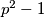 .
.
comment
Hi guys ,
Here is a nice problem:
Let be given a sequence such that
such that 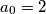 and
and 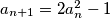 . Show that if
. Show that if  is an odd prime such that
is an odd prime such that 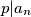 then we have
then we have 
Here are some futher question proposed by me :Prove or disprove that :
1)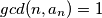
2) for every odd prime number we have
we have 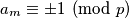 where
where 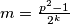 where
where 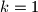 or
or 
Thanks kiu si u
Edited by Orl.
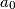 ,
,  ,
, 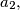
 is defined as follows:
is defined as follows: 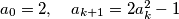 for
for 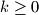 . Prove that if an odd prime
. Prove that if an odd prime  divides
divides  , then
, then 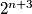 divides
divides 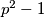 .
. comment
Hi guys ,
Here is a nice problem:
Let be given a sequence
 such that
such that 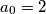 and
and 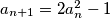 . Show that if
. Show that if  is an odd prime such that
is an odd prime such that 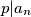 then we have
then we have 
Here are some futher question proposed by me :Prove or disprove that :
1)
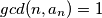
2) for every odd prime number
 we have
we have 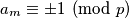 where
where 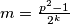 where
where 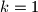 or
or 
Thanks kiu si u
Edited by Orl.
Let  be a prime number and let
be a prime number and let  be a set of positive integers that satisfies the following conditions: (1) the set of prime divisors of the elements in
be a set of positive integers that satisfies the following conditions: (1) the set of prime divisors of the elements in  consists of
consists of 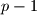 elements; (2) for any nonempty subset of
elements; (2) for any nonempty subset of  , the product of its elements is not a perfect
, the product of its elements is not a perfect  -th power. What is the largest possible number of elements in
-th power. What is the largest possible number of elements in  ?
?
 be a prime number and let
be a prime number and let  be a set of positive integers that satisfies the following conditions: (1) the set of prime divisors of the elements in
be a set of positive integers that satisfies the following conditions: (1) the set of prime divisors of the elements in  consists of
consists of 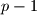 elements; (2) for any nonempty subset of
elements; (2) for any nonempty subset of  , the product of its elements is not a perfect
, the product of its elements is not a perfect  -th power. What is the largest possible number of elements in
-th power. What is the largest possible number of elements in  ?
?  Školjka
Školjka  and
and  be distinct integers greater than
be distinct integers greater than  . Prove that there exists a positive integer
. Prove that there exists a positive integer  such that
such that 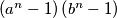 is not a perfect square.
is not a perfect square.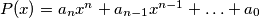 , where
, where 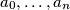 are integers,
are integers, 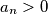 ,
, 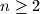 . Prove that there exists a positive integer
. Prove that there exists a positive integer  such that
such that 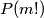 is a composite number.
is a composite number. 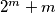 .
. 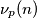 denote the exponent of
denote the exponent of 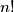 . Given
. Given 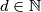 and
and 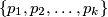 a set of
a set of  primes, show that there are infinitely many positive integers
primes, show that there are infinitely many positive integers 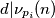 for all
for all 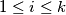 .
. 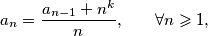 then
then 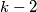 is divisible by
is divisible by  .
.