Neka je
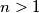
neparan cijeli broj pri čemu postoje cijeli brojevi
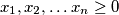
koji zadovoljavaju jednadžbe
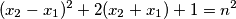
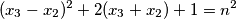

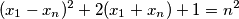
Pokažite da je ili
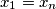
ili postoji
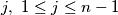
takav da je
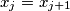
.
%V0
Neka je $n>1$ neparan cijeli broj pri čemu postoje cijeli brojevi $x_1, x_2, \ldots x_n \geq 0$ koji zadovoljavaju jednadžbe
$$ (x_2-x_1)^2+2(x_2+x_1)+1=n^2$$
$$ (x_3-x_2)^2+2(x_3+x_2)+1=n^2$$
$$ \ldots \ldots \ldots \ldots \ldots \ldots \ldots $$
$$ (x_1-x_n)^2+2(x_1+x_n)+1=n^2$$
Pokažite da je ili $x_1=x_n$ ili postoji $j, \ 1 \leq j \leq n-1$ takav da je $x_j=x_{j+1}$.