U trokutu

nalazi se točka

. Iz točke

spuštene su ortogonalne projekcije na stranice trokuta. Nožišta projekcija na

,

,

, označimo s

,

,

respektivno. Ako su četverokuti
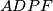
,
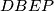
i
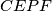
tangencijalni, dokaži da je

središte trokutu

upisane kružnice.
%V0
U trokutu $\triangle ABC$ nalazi se točka $P$. Iz točke $P$ spuštene su ortogonalne projekcije na stranice trokuta. Nožišta projekcija na $AB$, $BC$, $AC$, označimo s $D$,$E$,$F$ respektivno. Ako su četverokuti $ADPF$,$DBEP$ i $CEPF$ tangencijalni, dokaži da je $P$ središte trokutu $\triangle ABC$ upisane kružnice.