Slični zadaci
Unutar danog trokuta, čije opisana i upisana kružnica imaju središta  i
i  i polumjere
i polumjere  i
i  , nacrtane su četiri jednake kružnice polumjera
, nacrtane su četiri jednake kružnice polumjera  . Tri od njih diraju po dvije stranice trokuta te izvana diraju četvrtu kružnicu čije je središte u točki
. Tri od njih diraju po dvije stranice trokuta te izvana diraju četvrtu kružnicu čije je središte u točki  . Dokažite da točka
. Dokažite da točka  leži na pravcu određenom točkama
leži na pravcu određenom točkama  i
i  . Nađite polumjer
. Nađite polumjer  .
.
 i
i  i polumjere
i polumjere  i
i  , nacrtane su četiri jednake kružnice polumjera
, nacrtane su četiri jednake kružnice polumjera  . Tri od njih diraju po dvije stranice trokuta te izvana diraju četvrtu kružnicu čije je središte u točki
. Tri od njih diraju po dvije stranice trokuta te izvana diraju četvrtu kružnicu čije je središte u točki  . Dokažite da točka
. Dokažite da točka  leži na pravcu određenom točkama
leži na pravcu određenom točkama  i
i  . Nađite polumjer
. Nađite polumjer  .
.  Školjka
Školjka  je
je  promjer, a
promjer, a  i
i  , a
, a  presjek
presjek  i
i  . Dokaži da opisana kružnica trokutu
. Dokaži da opisana kružnica trokutu  siječe dužine
siječe dužine 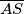 i
i 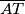 u polovištima.
u polovištima. 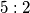 .
. 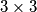 treba upisati prirodne brojeve, tako da u svakom retku i svakom stupcu produkt upisanih brojeva bude
treba upisati prirodne brojeve, tako da u svakom retku i svakom stupcu produkt upisanih brojeva bude 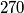 . Na koliko je načina to moguće napraviti?
. Na koliko je načina to moguće napraviti?  siječe stranice
siječe stranice  i
i 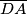 redom u točkama
redom u točkama  i
i  , a opisana kružnica trokuta
, a opisana kružnica trokuta 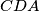 stranice
stranice  i
i  redom u točkama
redom u točkama 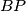 i
i 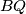 sijeku pravac
sijeku pravac 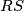 redom u točkama
redom u točkama  i
i  . Dokaži da točke
. Dokaži da točke 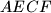 upisani su u istu kružnicu. Izrazite omjer njihovih površina pomoću duljina njihovih stranica.
upisani su u istu kružnicu. Izrazite omjer njihovih površina pomoću duljina njihovih stranica. 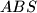 siječe pravac
siječe pravac 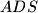 siječe pravac
siječe pravac