Dan je jednakokračan pravokutan trokut

s pravih kutom prvi vrhu

. Neka je

polovište hipotenuze, a

točka na hipotenuzi različita od

. Iz

povučena je okomica na hipotenuzu koja sječe stranicu

u točki

. Ako je

sjecište pravaca
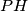
i
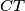
, dokažite da trokuti
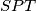
i
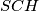
imaju iste površine.
%V0
Dan je jednakokračan pravokutan trokut $ABC$ s pravih kutom prvi vrhu $C$. Neka je $P$ polovište hipotenuze, a $T$ točka na hipotenuzi različita od $P$. Iz $T$ povučena je okomica na hipotenuzu koja sječe stranicu $\overline{AC}$ u točki $H$. Ako je $S$ sjecište pravaca $PH$ i $CT$, dokažite da trokuti $SPT$ i $SCH$ imaju iste površine.