na "cetvrtini" beskonacne kvadratne mreze ( tamo gdje je 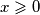 i
i 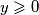 ), igra se sljedeca igra: u kvadraticima s koordinatama
), igra se sljedeca igra: u kvadraticima s koordinatama 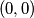 ,
, 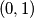 ,
, 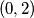 ,
, 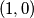 ,
, 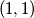 ,
, 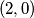 postavljen je po jedan zeton. dozvoljen potez je maknuti jedan zeton s polja
postavljen je po jedan zeton. dozvoljen potez je maknuti jedan zeton s polja 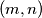 , gdje su
, gdje su 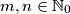 takvi da na poljima
takvi da na poljima 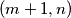 i
i 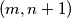 ne stoji zeton, te staviti po jedan zeton na polje
ne stoji zeton, te staviti po jedan zeton na polje 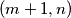 i na polje
i na polje 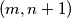 . je li moguce konacnom primjenom ovih poteza doci u situaciju da na pocetnih sest polja ne stoji vise niti jedan zeton?
. je li moguce konacnom primjenom ovih poteza doci u situaciju da na pocetnih sest polja ne stoji vise niti jedan zeton?
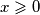 i
i 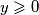 ), igra se sljedeca igra: u kvadraticima s koordinatama
), igra se sljedeca igra: u kvadraticima s koordinatama 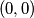 ,
, 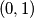 ,
, 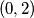 ,
, 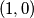 ,
, 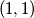 ,
, 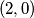 postavljen je po jedan zeton. dozvoljen potez je maknuti jedan zeton s polja
postavljen je po jedan zeton. dozvoljen potez je maknuti jedan zeton s polja 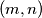 , gdje su
, gdje su 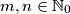 takvi da na poljima
takvi da na poljima 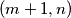 i
i 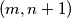 ne stoji zeton, te staviti po jedan zeton na polje
ne stoji zeton, te staviti po jedan zeton na polje 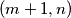 i na polje
i na polje 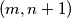 . je li moguce konacnom primjenom ovih poteza doci u situaciju da na pocetnih sest polja ne stoji vise niti jedan zeton?
. je li moguce konacnom primjenom ovih poteza doci u situaciju da na pocetnih sest polja ne stoji vise niti jedan zeton?  Školjka
Školjka