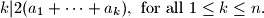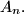na "cetvrtini" beskonacne kvadratne mreze ( tamo gdje je 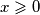 i
i 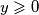 ), igra se sljedeca igra: u kvadraticima s koordinatama
), igra se sljedeca igra: u kvadraticima s koordinatama 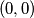 ,
, 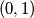 ,
, 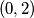 ,
, 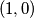 ,
, 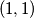 ,
, 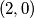 postavljen je po jedan zeton. dozvoljen potez je maknuti jedan zeton s polja
postavljen je po jedan zeton. dozvoljen potez je maknuti jedan zeton s polja 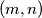 , gdje su
, gdje su 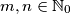 takvi da na poljima
takvi da na poljima 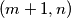 i
i 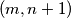 ne stoji zeton, te staviti po jedan zeton na polje
ne stoji zeton, te staviti po jedan zeton na polje 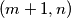 i na polje
i na polje 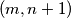 . je li moguce konacnom primjenom ovih poteza doci u situaciju da na pocetnih sest polja ne stoji vise niti jedan zeton?
. je li moguce konacnom primjenom ovih poteza doci u situaciju da na pocetnih sest polja ne stoji vise niti jedan zeton?
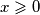 i
i 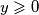 ), igra se sljedeca igra: u kvadraticima s koordinatama
), igra se sljedeca igra: u kvadraticima s koordinatama 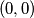 ,
, 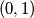 ,
, 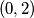 ,
, 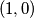 ,
, 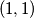 ,
, 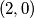 postavljen je po jedan zeton. dozvoljen potez je maknuti jedan zeton s polja
postavljen je po jedan zeton. dozvoljen potez je maknuti jedan zeton s polja 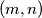 , gdje su
, gdje su 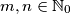 takvi da na poljima
takvi da na poljima 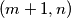 i
i 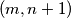 ne stoji zeton, te staviti po jedan zeton na polje
ne stoji zeton, te staviti po jedan zeton na polje 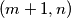 i na polje
i na polje 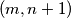 . je li moguce konacnom primjenom ovih poteza doci u situaciju da na pocetnih sest polja ne stoji vise niti jedan zeton?
. je li moguce konacnom primjenom ovih poteza doci u situaciju da na pocetnih sest polja ne stoji vise niti jedan zeton? Slični zadaci
Consider 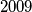 cards, each having one gold side and one black side, lying on parallel on a long table. Initially all cards show their gold sides. Two player, standing by the same long side of the table, play a game with alternating moves. Each move consists of choosing a block of
cards, each having one gold side and one black side, lying on parallel on a long table. Initially all cards show their gold sides. Two player, standing by the same long side of the table, play a game with alternating moves. Each move consists of choosing a block of 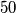 consecutive cards, the leftmost of which is showing gold, and turning them all over, so those which showed gold now show black and vice versa. The last player who can make a legal move wins.
consecutive cards, the leftmost of which is showing gold, and turning them all over, so those which showed gold now show black and vice versa. The last player who can make a legal move wins.
(a) Does the game necessarily end?
(b) Does there exist a winning strategy for the starting player?
Proposed by Michael Albert, Richard Guy, New Zealand
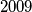 cards, each having one gold side and one black side, lying on parallel on a long table. Initially all cards show their gold sides. Two player, standing by the same long side of the table, play a game with alternating moves. Each move consists of choosing a block of
cards, each having one gold side and one black side, lying on parallel on a long table. Initially all cards show their gold sides. Two player, standing by the same long side of the table, play a game with alternating moves. Each move consists of choosing a block of 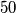 consecutive cards, the leftmost of which is showing gold, and turning them all over, so those which showed gold now show black and vice versa. The last player who can make a legal move wins.
consecutive cards, the leftmost of which is showing gold, and turning them all over, so those which showed gold now show black and vice versa. The last player who can make a legal move wins.(a) Does the game necessarily end?
(b) Does there exist a winning strategy for the starting player?
Proposed by Michael Albert, Richard Guy, New Zealand
This ISL 2005 problem has not been used in any TST I know. A pity, since it is a nice problem, but in its shortlist formulation, it is absolutely incomprehensible. Here is a mathematical restatement of the problem:
Let be a nonnegative integer.
be a nonnegative integer.
A forest consists of rooted (i. e. oriented) trees. Each vertex of the forest is either a leaf or has two successors. A vertex is called an extended successor of a vertex
is called an extended successor of a vertex 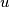 if there is a chain of vertices
if there is a chain of vertices 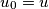 ,
, 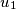 ,
, 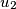 , ...,
, ..., 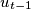 ,
, 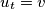 with
with 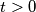 such that the vertex
such that the vertex 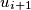 is a successor of the vertex
is a successor of the vertex 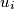 for every integer
for every integer  with
with 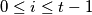 . A vertex is called dynastic if it has two successors and each of these successors has at least
. A vertex is called dynastic if it has two successors and each of these successors has at least  extended successors.
extended successors.
Prove that if the forest has vertices, then there are at most
vertices, then there are at most 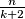 dynastic vertices.
dynastic vertices.
Let
 be a nonnegative integer.
be a nonnegative integer.A forest consists of rooted (i. e. oriented) trees. Each vertex of the forest is either a leaf or has two successors. A vertex
 is called an extended successor of a vertex
is called an extended successor of a vertex 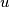 if there is a chain of vertices
if there is a chain of vertices 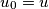 ,
, 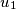 ,
, 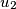 , ...,
, ..., 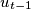 ,
, 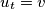 with
with 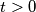 such that the vertex
such that the vertex 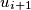 is a successor of the vertex
is a successor of the vertex 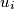 for every integer
for every integer  with
with 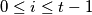 . A vertex is called dynastic if it has two successors and each of these successors has at least
. A vertex is called dynastic if it has two successors and each of these successors has at least  extended successors.
extended successors.Prove that if the forest has
 vertices, then there are at most
vertices, then there are at most 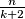 dynastic vertices.
dynastic vertices. There are 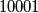 students at an university. Some students join together to form several clubs (a student may belong to different clubs). Some clubs join together to form several societies (a club may belong to different societies). There are a total of
students at an university. Some students join together to form several clubs (a student may belong to different clubs). Some clubs join together to form several societies (a club may belong to different societies). There are a total of  societies. Suppose that the following conditions hold:
societies. Suppose that the following conditions hold:
i.) Each pair of students are in exactly one club.
ii.) For each student and each society, the student is in exactly one club of the society.
iii.) Each club has an odd number of students. In addition, a club with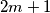 students (
students ( is a positive integer) is
is a positive integer) is
in exactly societies.
societies.
Find all possible values of .
.
RemarkIn IMOTC 2005, it is given that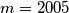 .
.
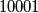 students at an university. Some students join together to form several clubs (a student may belong to different clubs). Some clubs join together to form several societies (a club may belong to different societies). There are a total of
students at an university. Some students join together to form several clubs (a student may belong to different clubs). Some clubs join together to form several societies (a club may belong to different societies). There are a total of  societies. Suppose that the following conditions hold:
societies. Suppose that the following conditions hold: i.) Each pair of students are in exactly one club.
ii.) For each student and each society, the student is in exactly one club of the society.
iii.) Each club has an odd number of students. In addition, a club with
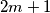 students (
students ( is a positive integer) is
is a positive integer) is in exactly
 societies.
societies. Find all possible values of
 .
. RemarkIn IMOTC 2005, it is given that
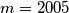 .
. For  an odd positive integer, the unit squares of an
an odd positive integer, the unit squares of an 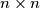 chessboard are coloured alternately black and white, with the four corners coloured black. A it tromino is an
chessboard are coloured alternately black and white, with the four corners coloured black. A it tromino is an  -shape formed by three connected unit squares. For which values of
-shape formed by three connected unit squares. For which values of  is it possible to cover all the black squares with non-overlapping trominos? When it is possible, what is the minimum number of trominos needed?
is it possible to cover all the black squares with non-overlapping trominos? When it is possible, what is the minimum number of trominos needed?
 an odd positive integer, the unit squares of an
an odd positive integer, the unit squares of an 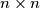 chessboard are coloured alternately black and white, with the four corners coloured black. A it tromino is an
chessboard are coloured alternately black and white, with the four corners coloured black. A it tromino is an  -shape formed by three connected unit squares. For which values of
-shape formed by three connected unit squares. For which values of  is it possible to cover all the black squares with non-overlapping trominos? When it is possible, what is the minimum number of trominos needed?
is it possible to cover all the black squares with non-overlapping trominos? When it is possible, what is the minimum number of trominos needed?  Školjka
Školjka 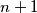 prirodnih brojeva čiji je zbroj
prirodnih brojeva čiji je zbroj 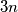 i oni su poredani u krug. Dokaži da postoji nekoliko uzastopnih brojeva (moguće i samo
i oni su poredani u krug. Dokaži da postoji nekoliko uzastopnih brojeva (moguće i samo  ) čiji je zbroj jednak točno
) čiji je zbroj jednak točno  .
. 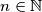 and
and 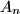 set of all permutations
set of all permutations  of the set
of the set 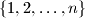 for which
for which