Slični zadaci
Given  points in a plane, no three of them being collinear. Each two of these
points in a plane, no three of them being collinear. Each two of these  points are joined with a segment, and every of these segments is painted either red or blue; assume that there is no triangle whose sides are segments of equal color.
points are joined with a segment, and every of these segments is painted either red or blue; assume that there is no triangle whose sides are segments of equal color.
a.) Show that:
(1) Among the four segments originating at any of the points, two are red and two are blue.
points, two are red and two are blue.
(2) The red segments form a closed way passing through all given points. (Similarly for the blue segments.)
given points. (Similarly for the blue segments.)
b.) Give a plan how to paint the segments either red or blue in order to have the condition (no triangle with equally colored sides) satisfied.
 points in a plane, no three of them being collinear. Each two of these
points in a plane, no three of them being collinear. Each two of these  points are joined with a segment, and every of these segments is painted either red or blue; assume that there is no triangle whose sides are segments of equal color.
points are joined with a segment, and every of these segments is painted either red or blue; assume that there is no triangle whose sides are segments of equal color. a.) Show that:
(1) Among the four segments originating at any of the
 points, two are red and two are blue.
points, two are red and two are blue. (2) The red segments form a closed way passing through all
 given points. (Similarly for the blue segments.)
given points. (Similarly for the blue segments.) b.) Give a plan how to paint the segments either red or blue in order to have the condition (no triangle with equally colored sides) satisfied.
 Školjka
Školjka  of five points in the plane, no three of them being collinear, let
of five points in the plane, no three of them being collinear, let 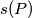 be the numbers of acute triangles formed by vertices in
be the numbers of acute triangles formed by vertices in 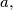
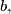
 of a triangle
of a triangle  form an arithmetical progression (such that
form an arithmetical progression (such that 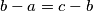 ). The side lengths
). The side lengths 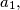
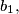
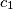 of a triangle
of a triangle 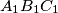 also form an arithmetical progression (with
also form an arithmetical progression (with 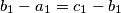 ). (Hereby,
). (Hereby, 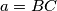 ,
, 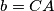 ,
, 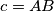 ,
, 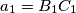 ,
, 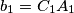 ,
, 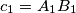 .) Moreover, we know that
.) Moreover, we know that 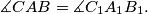
 -gon
-gon 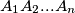 (with
(with 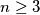 ) in a plane. How many triangles of the kind
) in a plane. How many triangles of the kind 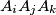 are obtuse ?
are obtuse ?  and the centroid
and the centroid  of a triangle
of a triangle  such that all the angles of the triangle lie in the interval
such that all the angles of the triangle lie in the interval ![[40^\circ, 70^\circ].](/media/m/9/a/d/9adb384f374eb62fabd3675b69323b53.png)
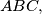 let
let 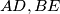 be altitudes and
be altitudes and 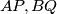 internal bisectors. Denote by
internal bisectors. Denote by  and
and  the incenter and the circumcentre of the triangle, respectively. Prove that the points
the incenter and the circumcentre of the triangle, respectively. Prove that the points 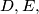 and
and 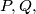 and
and