A tetrahedron is called a MEMO-tetrahedron if all six sidelengths are different positive integers where one of them is  and one of them is
and one of them is  . Let
. Let 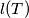 be the sum of the sidelengths of the tetrahedron
be the sum of the sidelengths of the tetrahedron  .
.
(a) Find all positive integers so that there exists a MEMO-Tetrahedron
so that there exists a MEMO-Tetrahedron  with
with 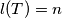 .
.
(b) How many pairwise non-congruent MEMO-tetrahedrons satisfying
satisfying 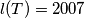 exist? Two tetrahedrons are said to be non-congruent if one cannot be obtained from the other by a composition of reflections in planes, translations and rotations. (It is not neccessary to prove that the tetrahedrons are not degenerate, i.e. that they have a positive volume).
exist? Two tetrahedrons are said to be non-congruent if one cannot be obtained from the other by a composition of reflections in planes, translations and rotations. (It is not neccessary to prove that the tetrahedrons are not degenerate, i.e. that they have a positive volume).
 and one of them is
and one of them is  . Let
. Let 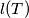 be the sum of the sidelengths of the tetrahedron
be the sum of the sidelengths of the tetrahedron  .
. (a) Find all positive integers
 so that there exists a MEMO-Tetrahedron
so that there exists a MEMO-Tetrahedron  with
with 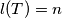 .
. (b) How many pairwise non-congruent MEMO-tetrahedrons
 satisfying
satisfying 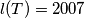 exist? Two tetrahedrons are said to be non-congruent if one cannot be obtained from the other by a composition of reflections in planes, translations and rotations. (It is not neccessary to prove that the tetrahedrons are not degenerate, i.e. that they have a positive volume).
exist? Two tetrahedrons are said to be non-congruent if one cannot be obtained from the other by a composition of reflections in planes, translations and rotations. (It is not neccessary to prove that the tetrahedrons are not degenerate, i.e. that they have a positive volume).  Školjka
Školjka