Consider a 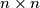 checkerboard with
checkerboard with 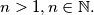 How many possibilities are there to put
How many possibilities are there to put 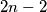 identical pebbles on the checkerboard (each on a different field/place) such that no two pebbles are on the same checkerboard diagonal. Two pebbles are on the same checkerboard diagonal if the connection segment of the midpoints of the respective fields are parallel to one of the diagonals of the
identical pebbles on the checkerboard (each on a different field/place) such that no two pebbles are on the same checkerboard diagonal. Two pebbles are on the same checkerboard diagonal if the connection segment of the midpoints of the respective fields are parallel to one of the diagonals of the 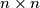 square.
square.
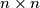 checkerboard with
checkerboard with 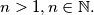 How many possibilities are there to put
How many possibilities are there to put 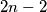 identical pebbles on the checkerboard (each on a different field/place) such that no two pebbles are on the same checkerboard diagonal. Two pebbles are on the same checkerboard diagonal if the connection segment of the midpoints of the respective fields are parallel to one of the diagonals of the
identical pebbles on the checkerboard (each on a different field/place) such that no two pebbles are on the same checkerboard diagonal. Two pebbles are on the same checkerboard diagonal if the connection segment of the midpoints of the respective fields are parallel to one of the diagonals of the 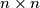 square.
square.  Školjka
Školjka