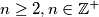
On a blackboard there are numbers. In each step we select two numbers from the blackboard and replace both of them by their sum. Determine all numbers for which it is possible to yield identical number after a finite number of steps.
%V0
On a blackboard there are $n \geq 2, n \in \mathbb{Z}^{+}$ numbers. In each step we select two numbers from the blackboard and replace both of them by their sum. Determine all numbers $n$ for which it is possible to yield $n$ identical number after a finite number of steps.
Izvor: Srednjoeuropska matematička olimpijada 2008, ekipno natjecanje, problem 6
Školjka 
numbers. In each step we select two numbers from the blackboard and replace both of them by their sum. Determine all numbers 
for which it is possible to yield