Let

be an acute-angled triangle. Let

be a point such

and

are on distinct sides of the line

, and

is an interior point of segment

. We have
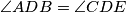
,
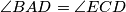
, and
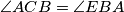
. Prove that

,

and

lie on the same line.
%V0
Let $ABC$ be an acute-angled triangle. Let $E$ be a point such $E$ and $B$ are on distinct sides of the line $AC$, and $D$ is an interior point of segment $AE$. We have $\angle ADB = \angle CDE$, $\angle BAD = \angle ECD$, and $\angle ACB = \angle EBA$. Prove that $B$, $C$ and $E$ lie on the same line.