Let

be a convex quadrilateral such that

and

are not parallel and
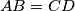
. The midpoints of the diagonals

and
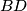
are

and

, respectively. The line
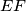
meets segments

and

at
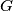
and
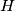
, respectively. Show that
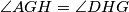
.
%V0
Let $ABCD$ be a convex quadrilateral such that $AB$ and $CD$ are not parallel and $AB=CD$. The midpoints of the diagonals $AC$ and $BD$ are $E$ and $F$, respectively. The line $EF$ meets segments $AB$ and $CD$ at $G$ and $H$, respectively. Show that $\angle AGH = \angle DHG$.