Let
be a convex quadrilateral such that
and
are not parallel and
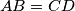
. The midpoints of the diagonals
and
are
and
, respectively. The line
meets segments
and
at
and
, respectively. Show that
.
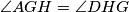
%V0
Let $ABCD$ be a convex quadrilateral such that $AB$ and $CD$ are not parallel and $AB=CD$. The midpoints of the diagonals $AC$ and $BD$ are $E$ and $F$, respectively. The line $EF$ meets segments $AB$ and $CD$ at $G$ and $H$, respectively. Show that $\angle AGH = \angle DHG$.
Školjka