Slični zadaci
Initially, only the integer 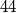 is written on a board. An integer a on the board can be re- placed with four pairwise different integers
is written on a board. An integer a on the board can be re- placed with four pairwise different integers 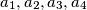 such that the arithmetic mean
such that the arithmetic mean 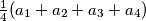 of the four new integers is equal to the number
of the four new integers is equal to the number  . In a step we simultaneously replace all the integers on the board in the above way. After
. In a step we simultaneously replace all the integers on the board in the above way. After 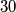 steps we end up with
steps we end up with 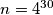 integers
integers 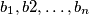 on the board. Prove that
on the board. Prove that 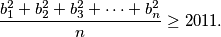
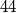 is written on a board. An integer a on the board can be re- placed with four pairwise different integers
is written on a board. An integer a on the board can be re- placed with four pairwise different integers 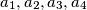 such that the arithmetic mean
such that the arithmetic mean 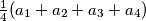 of the four new integers is equal to the number
of the four new integers is equal to the number  . In a step we simultaneously replace all the integers on the board in the above way. After
. In a step we simultaneously replace all the integers on the board in the above way. After 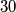 steps we end up with
steps we end up with 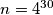 integers
integers 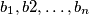 on the board. Prove that
on the board. Prove that 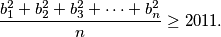
 Školjka
Školjka  ,
,  be real numbers such that for every two of the equations
be real numbers such that for every two of the equations 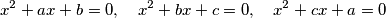 there is exactly one real number satisfying both of them. Determine all possible values of
there is exactly one real number satisfying both of them. Determine all possible values of 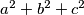 .
. 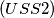 Prove that for
Prove that for 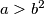 , the identity
, the identity 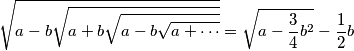 holds.
holds. 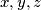 be real numbers each of whose absolute value is different from
be real numbers each of whose absolute value is different from 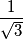 such that
such that 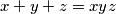 . Prove that
. Prove that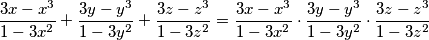
 be a polynomial with real coefficients such that
be a polynomial with real coefficients such that 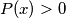 if
if 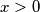 . Prove that there exist polynomials
. Prove that there exist polynomials  and
and  with nonnegative coefficients such that
with nonnegative coefficients such that 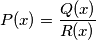 if
if 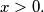
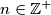 and let
and let 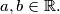 Determine the range of
Determine the range of 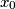 for which
for which 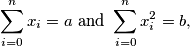
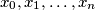 are real variables.
are real variables.  ,
,  ,
,  be real numbers satisfying
be real numbers satisfying 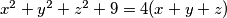 . Prove that
. Prove that 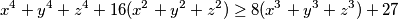 and determine when equality holds.
and determine when equality holds.