Konačan broj polja beskonačne kvadratne mreže obojan je crnom bojom. Dokažite da je u toj ravnini moguće odabrati konačno mnogo kvadrata koji zadovoljavaju svaki od sljedećih uvjeta:
 Unutrašnjosti svaka dva različita kvadrata su disjunktne (imaju prazan presjek).
Unutrašnjosti svaka dva različita kvadrata su disjunktne (imaju prazan presjek).
 Svako crno obojeno polje leži u nekom od tih kvadrata.
Svako crno obojeno polje leži u nekom od tih kvadrata.
 Površina crnih polja u svakom od odabranih kvadrata je barem
Površina crnih polja u svakom od odabranih kvadrata je barem  , a najvise
, a najvise  površine tog kvadrata.
površine tog kvadrata.
 Unutrašnjosti svaka dva različita kvadrata su disjunktne (imaju prazan presjek).
Unutrašnjosti svaka dva različita kvadrata su disjunktne (imaju prazan presjek).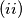 Svako crno obojeno polje leži u nekom od tih kvadrata.
Svako crno obojeno polje leži u nekom od tih kvadrata.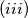 Površina crnih polja u svakom od odabranih kvadrata je barem
Površina crnih polja u svakom od odabranih kvadrata je barem  , a najvise
, a najvise  površine tog kvadrata.
površine tog kvadrata.  Školjka
Školjka