Let  be a positive integer. A square
be a positive integer. A square  is partitioned into
is partitioned into 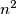 unit squares. Each of them is divided into two triangles by the diagonal parallel to
unit squares. Each of them is divided into two triangles by the diagonal parallel to  . Some of the vertices of the unit squares are colored red in such a way that each of these
. Some of the vertices of the unit squares are colored red in such a way that each of these 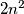 triangles contains at least one red vertex. Find the least number of red vertices.
triangles contains at least one red vertex. Find the least number of red vertices.
 be a positive integer. A square
be a positive integer. A square  is partitioned into
is partitioned into 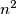 unit squares. Each of them is divided into two triangles by the diagonal parallel to
unit squares. Each of them is divided into two triangles by the diagonal parallel to  . Some of the vertices of the unit squares are colored red in such a way that each of these
. Some of the vertices of the unit squares are colored red in such a way that each of these 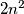 triangles contains at least one red vertex. Find the least number of red vertices.
triangles contains at least one red vertex. Find the least number of red vertices.  Školjka
Školjka