We call a positive integer

amazing if there exist positive integers
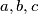
such that the equality
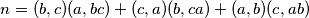
holds. Prove that there exist
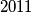
consecutive positive integers which are amazing.
Note. By
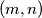
we denote the greatest common divisor of positive integers

and

.
%V0
We call a positive integer $n$ amazing if there exist positive integers $a, b, c$ such that the equality $$n = (b, c)(a, bc) + (c, a)(b, ca) + (a, b)(c, ab)$$ holds. Prove that there exist $2011$ consecutive positive integers which are amazing.
Note. By $(m, n)$ we denote the greatest common divisor of positive integers $m$ and $n$.
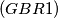 The polynomial
The polynomial 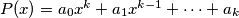 , where
, where 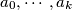 are integers, is said to be divisible by an integer
are integers, is said to be divisible by an integer  if
if  is a multiple of
is a multiple of  for every integral value of
for every integral value of  . Show that if
. Show that if  is divisible by
is divisible by  , then
, then 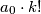 is a multiple of
is a multiple of  . Also prove that if
. Also prove that if 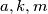 are positive integers such that
are positive integers such that 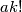 is a multiple of
is a multiple of  , then a polynomial
, then a polynomial  with leading term
with leading term 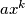 can be found that is divisible by
can be found that is divisible by 
 Školjka
Školjka  amazing if there exist positive integers
amazing if there exist positive integers 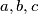 such that the equality
such that the equality 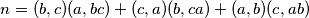 holds. Prove that there exist
holds. Prove that there exist 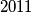 consecutive positive integers which are amazing.
consecutive positive integers which are amazing.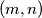 we denote the greatest common divisor of positive integers
we denote the greatest common divisor of positive integers  Consider the integer
Consider the integer 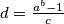 , where
, where 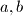 , and
, and  are positive integers and
are positive integers and 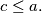 Prove that the set
Prove that the set  of integers that are between
of integers that are between  and
and  and relatively prime to
and relatively prime to 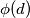 ) can be partitioned into
) can be partitioned into  elements. What can be said about the rational number
elements. What can be said about the rational number 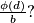
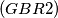 Let
Let 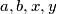 be positive integers such that
be positive integers such that  and
and 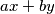 is
is 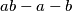 . If
. If 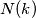 is the largest number not expressible in the form
is the largest number not expressible in the form  ways, find
ways, find 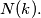
 is a multiple of
is a multiple of 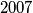 .
.  and
and  be disjoint nonempty sets with
be disjoint nonempty sets with 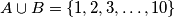 . Show that there exist elements
. Show that there exist elements 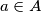 and
and 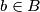 such that the number
such that the number 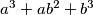 is divisible by
is divisible by 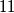 .
.