Jedno od žarišta (fokusa) elipse
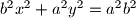
je žarište parabole
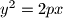
, a pravac
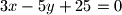
je njihova zajednička tangenta. Dokaži da je trokut kojeg određuju zajedničko žarište i dva dirališta tangente pravokutan.
%V0
Jedno od žarišta (fokusa) elipse $b^2x^2+a^2y^2=a^2b^2$ je žarište parabole $y^2=2px$, a pravac $3x-5y+25=0$ je njihova zajednička tangenta. Dokaži da je trokut kojeg određuju zajedničko žarište i dva dirališta tangente pravokutan.