Niz
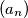
zadan je rekurzivno:
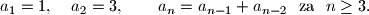
Dokaži da vrijedi nejednakost
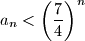
za sve

.
%V0
Niz $(a_n)$ zadan je rekurzivno: $$
a_1=1, \quad a_2=3, \qquad a_n=a_{n-1}+a_{n-2} \ \text{ za } \ n\geq 3.
$$ Dokaži da vrijedi nejednakost $a_n<\left(\dfrac{7}{4}\right)^n$ za sve $n \in \mathbb{N}$.