Produkt pozitivnih realnih brojeva

,

i

jednak je

. Ako je
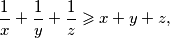
dokažite da je
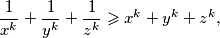
za svaki prirodan broj

.
%V0
Produkt pozitivnih realnih brojeva $x$, $y$ i $z$ jednak je $1$. Ako je $$\frac{1}{x} + \frac{1}{y} + \frac{1}{z} \geqslant x + y + z \text{,}$$ dokažite da je $$\frac{1}{x^k} + \frac{1}{y^k} + \frac{1}{z^k} \geqslant x^k + y^k + z^k \text{,}$$ za svaki prirodan broj $k$.